뉴스
"증명"(으)로 총 1,892건 검색되었습니다.

- 스마트폰 세상에서 아이들 눈 건강 지키는 10가지 방법2018.08.19
- 태블릿 PC와 같은 전자기기 사용의 증가에 있지 않을까 싶은데요. 물론 과학적으로 증명된 바는 아직 없습니다. 하지만 확실한 것은 각종 전자기기의 사용으로 스크린에 많이 노출될수록 눈의 피로도는 올라간다는 것입니다. 바로 눈의 건조함, 긴장, 그로 인한 두통 및 사물이 흐릿하게 보이는 ... ...
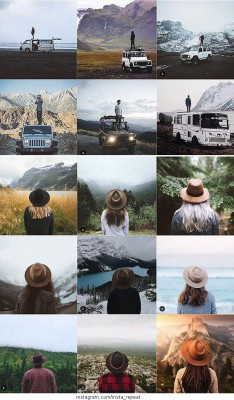
- 문제는 창의력, SNS 사진은 다 비슷해팝뉴스 l2018.08.05
- 다양하지 않다. 비슷비슷한 사진들이 너무 많다. 미국의 한 네티즌이 인스타그램을 통해 증명한 사실이다. 사람들이 풍경 사진을 촬영하는 방식, 텐트에서 자연 풍경을 담는 앵글, 밤하늘을 촬영하는 기법 등은 다 비슷했다. 전혀 다른 사람이 전혀 다른 시기에 촬영한 사진들인데 거의 다를 바가 ... ...
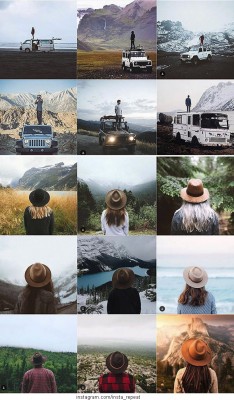
- 문제는 창의력, SNS 사진은 다 비슷해팝뉴스 l2018.08.03
- 다양하지 않다. 비슷비슷한 사진들이 너무 많다. 미국의 한 네티즌이 인스타그램을 통해 증명한 사실이다. 사람들이 풍경 사진을 촬영하는 방식, 텐트에서 자연 풍경을 담는 앵글, 밤하늘을 촬영하는 기법 등은 다 비슷했다. 전혀 다른 사람이 전혀 다른 시기에 촬영한 사진들인데 거의 다를 바가 ... ...

- 쿠르드 출신 수학자, 7세에 이진법 배운 천재...4인 4색 2018 필즈상수학동아 l2018.08.03
- 집합) 안에 ‘파노 다양체’라는 특이한 다양체가 드물게 있다”는 내용의 BAB추측을 증명해 수상의 영예를 얻었다. 브라질 리우데자네이루에서 열린 세계수학재대회 장면. -김우현 기자 제공 이탈리아 출신의 피갈리 교수는 물건을 효율적으로 운송하는 경로를 찾는 ‘최적 운송 이론’으로 ... ...
- 난치병 ’파킨슨‘ 치료법 찾아냈다동아사이언스 l2018.07.29
- 수 있다. 연구진은 실험용 쥐를 이용한 동물실험으로 세리아 입자의 효과를 실제로 증명했다. 파킨슨에 걸린 쥐에게 3종류의 세리아 입자를 주입한 결과, 뇌 속 신경전달물질인 도파민의 원료 물질인 ‘티로신하이드록시아제(TH)’의 양이 정상쥐와 비슷한 수준으로 올라갔다. 세포 외부용으로 ... ...

- 한국의 코워킹스페이스, “효용성 높고, 네트워킹에 아쉬워”2018.07.26
- 14.8%나 됩니다. 스타트업들이 처음 얻는 사무실로 코워킹 스페이스가 인기있다는 것을 증명하는 수치입니다. 그런데 요즘 들어서 조금 다른 움직임도 있다고 합니다. 대기업이나 글로벌 기업의 입주 사례가 늘면서 100명 이상, 혹은 아예 한 층을 통째로 이용하는 사례가 늘어나는 추세라고 합니다. ... ...

- [별별 필즈상 이야기] 필즈상 받고 싶은데 갈 수가 없어요!동아사이언스 l2018.07.17
- 논문은 앤드루 와일스가 41세 되던 이듬해 출판됐다. 평생의 꿈인 페르마의 정리를 증명한 것에 만족하며 아쉬움을 달래던 앤드루 와일스는 1998년 뜻밖의 기쁜 소식을 듣게 된다. 국제수학연맹에서 그를 위해 특별 공로상과 기념 은판을 제작해 주기로 한 것이다. *출처: 수학동아 2014년 8월호 ... ...

- [별별 필즈상 이야기] 필즈상? 저는 안 받을래요!동아사이언스 l2018.07.16
- 그리고리 페렐만이다. 페렐만은 100년 동안 풀리지 않은 난제인 ‘푸앵카레 추측’을 증명한 수학자로, 2006년 스페인에서 열린 세계수학자대회에서 필즈상 수상자로 결정됐다. 하지만 그는 “문제를 풀었으면 됐지 상은 필요 없다”는 말을 남기고 시상식 참석을 거절했다. 푸앵카레 추측은 영국 ... ...
- [강석기의 과학카페] 동물 다세포성의 기원에 대한 고찰2018.07.10
- 별 차이가 없었다. 정상세포에 비해 단세포성이 커진 게 암세포라는 걸 증명하는 실험 데이터다. 사람 유전자를 진화 역사에 따라 16단계로 분류한 뒤 각각의 유전자 발현패턴을 비교해보면 암세포에서 단세포 유전자(1~3단계)는 발현량이 는 반면 다세포 유전자는 줄거나(4~11) 변화가 없다(12~16). ... ...

- [2018년 필즈상] 미분기하학 분야 필즈상 0순위, 시몬 브렌들수학동아 l2018.07.09
- 3차원으로 확장한 3차원 초구에서는 이런 비눗방울이 있다는 걸 2012년에 브렌들 교수가 증명했습니다. 페렐만의 연구에서 아이디어 얻어 브렌들 교수의 또 다른 업적인 평균 곡률 흐름은 푸앵카레 추측(3차원 공간의 모든 폐곡선이 한 점으로 모일 수 있다면 그 공간은 구로 바꿀 수 있다)과 ... ...
이전121122123124125126127128129 다음

















