뉴스
"값"(으)로 총 1,558건 검색되었습니다.

- 도심 에너지원 재생에너지로 전환하는 도시 구현법동아사이언스 l2024.09.11
- 생산한 잉여 전력을 전력망으로 내보내지 않고 직접 사용하는 비율을 말한다. 이 비율 값이 클수록 전력망의 안정적 운영에 기여한다. 특히 실증에 적용된 연간 에너지 소비량은 107메가와트시(MWh)로 해외 선진기관의 시뮬레이션 기반 연구보다 7배 큰 규모로 진행돼 실제 도시 환경 적용 가능성을 ... ...

- 체질량지수 용도폐기?…전문가들 "둥글기 지수를 건강지표로 활용해야"동아사이언스 l2024.09.08
- 게 전문가들의 조언이다. Avilika/게티이미지뱅크 제공. 몸무게를 키의 제곱으로 나눈 값인 ‘체질량지수(BMI)’는 비만과 건강을 평가하는 지표로 오랫동안 사용돼왔다. 과체중, 비만, 고도비만 등을 분류하는 가장 널리 알려진 건강 지표지만 결함이 있다는 비판을 동시에 받고 있다. 올해 ... ...

- 인공지능으로 이온 농도 예측해 깨끗한 물 만든다동아사이언스 l2024.09.08
- 데 활용했다. 랜덤포레스트는 AI 기술의 일종으로 다양한 입력 인자에 따른 예측 인자의 값을 정량적으로 예측하는데 널리 활용된다. 연구팀인 개발한 랜덤포레스트 기반 AI 모델은 처리수의 전기전도도 및 각 이온의 농도(Na⁺, K⁺, Ca2⁺, Cl⁻)를 정밀하게 예측할 수 있었다. 랜덤포레스트 모델은 ... ...

- 韓 독자 '양자컴퓨터 오류 정정' 기술 개발…"전세계서 가장 앞서"동아사이언스 l2024.08.29
- ' 기법을 활용해 양자컴퓨팅 구조를 설계했다. 연구팀이 개발한 방식은 실험 결과 임계값이 최대 14%까지 구현 가능하다는 것이 확인됐다. 현재 전 세계 광기반 범용 양자컴퓨팅 시스템에서 가장 높은 기록이다. 광기반 양자컴퓨팅의 자원인 광자(빛 입자)를 같은 양 소모했을 때 사이퀀텀의 방식보다 ... ...

- 구명조끼를 입으면 왜 몸이 뜰까어린이과학동아 l2024.08.17
- 있고 나머지는 물보다 밀도가 조금 낮기 때문이에요. 밀도는 물질의 질량을 부피로 나눈 값으로 물체의 빽빽한 정도를 나타냅니다. 부피가 커질수록 밀도가 낮아집니다. 밀도는 물질마다 다른데 밀도가 다른 두 물질이 만나면 밀도가 큰 물질이 가라앉고 밀도가 작은 물질이 뜹니다. 물과 우리몸을 ... ...
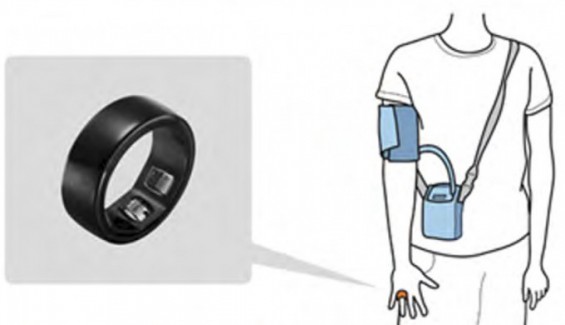
- 밤시간 안정적으로 혈압 측정하는 '스마트 반지'동아사이언스 l2024.08.13
- 29.9%였다. 모바일 디바이스 혈압 측정기는 사용의 편리함, 다양한 환경에서의 혈압값 확보, 장시간 측정 등의 이점이 있어 고혈압 환자들이 일상에서 혈압을 관리하고 개선하기에도 유리하다. 이 교수는 “향후 모바일 디바이스 혈압 측정 기술은 고혈압의 예방 및 조절에 중요한 기술로 자리 ... ...
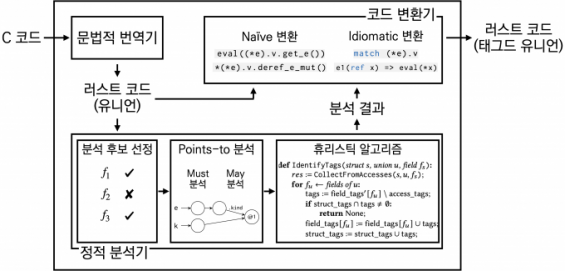
- 美 국방부 과제 'C언어 번역 기술' 韓 연구팀이 선도동아사이언스 l2024.08.13
- 검사하기 때문에 메모리 문제를 탐지하고 예방할 수 있다. 연구팀은 각 유니언의 태그값이 저장된 위치를 찾는 프로그램 분석 기법과 분석 결과를 통해 유니언을 태그드 유니언으로 대체하는 변환 기법을 개발했다. 실제 C언어로 쓰인 프로그램 번역에 적용한 결과 정확하고 효율적으로 유니언을 ... ...

- 혹한에도 끄떡없는 이차전지용 하이브리드 전극 소재동아사이언스 l2024.08.13
- 격자 구조를 찾고 리튬의 흡착 위치를 예측해 최대 용량과 전압을 계산했다. 그 결과 예측값이 실험에서 도출된 결과와 들어맞는 것을 확인하고 SKIER-5가 전극 소재로 적합하다는 것을 입증했다. 연구진은 “SKIER-5는 전지 산업에 핵심적인 역할을 할 수 있는 원천 소재로 기존 음극재로 사용되는 ... ...

- [과기원NOW] KAIST, 청소기·헤어드라이어 소음 줄이는 기술 개발 外동아사이언스 l2024.08.06
- 소음은 차단되는 ‘복소 임피던스 타일’을 개발했다. 음향 임피던스를 원하는 복소수 값으로 조절할 수 있는 신개념 음향 메타물질이다. 음향 임피던스는 소리가 전파되는 매질이 가진 고유의 음향적 특성이다. 연구팀은 헤어드라이어, 청소기 등 전자제품이나 미래 교통 수단 등의 소음 저감의 ... ...

- 중국서 쌓인 눈 높이로 한국 폭염 예측하는 AI동아사이언스 l2024.08.06
- 있는 AI 기술이다. 이 기술로 양의 값을 가지면 입력변수가 예측 결과를 증가시키고 음의 값을 가지면 예측 결과를 감소시키는 패턴을 알아낼 수 있다. 연구팀의 분석 결과 겨울철 톈산산맥의 적설 깊이 증가와 봄철 몽골과 중국에 걸쳐 있는 고비사막의 적설 깊이의 감소가 한국의 여름철 폭염을 ... ...
이전8910111213141516 다음

















