뉴스
"보기"(으)로 총 2,635건 검색되었습니다.

- [표지로 읽는 과학]그린란드에 살던 바이킹 후손들은 15세기 왜 갑자기 사라졌을까?동아사이언스 l2016.11.14
- 애썼다. 기후변화가 절멸에 영향을 준 것은 맞지만 어리석게도 적응에 실패했다고 보기는 어렵다는 결론이다. 연구진은 “그들은 제대로 된 방향으로 갔지만 어쨌든 실패했다”고 밝혔다. 네이처 제공 ‘네이처’ 10일자 표지에는 뉴런(신경세포)의 끊어진 부위가 다시 연결되는 모습을 ... ...

- 벤츠 버리고 달아난 만취 운전자 2016.11.13
- 팝뉴스 제공 아주 보기 힘든 장면일 것이다. 고급차가 버려져 있다. 그것도 철길이다. 열차 운행은 멈췄고 시민들과 관계 당국 모두 어리둥절했다. 신형 벤츠 차량은 현지 일자 일요일 아침 7시 영국 버밍엄 스노우힐 인근의 철로에서 발견되었다. 주인은 없었다. 차주는 차를 버리고 달아나 버렸다. ... ...

- 키스하는 얼굴 조각상이 화성 표면에? 2016.11.13
- 보면 자연석이 아닌 것 같다. 지능과 예술혼을 가진 존재가 다듬은 것처럼 보인다. 보기에 따라서는 입술을 내밀고 키스를 하려는 존재의 얼굴 같다. 물론 착시이고 우연일 수 있다. 하지만 일부 네티즌들은 동요하고 호기심을 나타낸다. 키스 조각상을 본 그들은 화성에도 클림트 같은 조각가가 ... ...

- 동물병원에서 예방접종을 너무 많이 권합니다. 전부 다 해야 하나요?동아사이언스 l2016.11.13
- 한 번 더 확인하는 것이 안전합니다. 다시 원래 대로 이야기로 돌아옵시다. 얼핏 보기만 해도 많습니다. 종합, 코로나, 켄넬코프, 인플루엔자, 광견병 5종류를 매년 맞추고, 시기에 맞춰 구충제와 사상충 약도 먹이고, 필요할 땐 외부기생충 방제제도 사용합니다. 머리가 아파옵니다. 본인의 나이와 ... ...

- 괴수 같은 ‘공포의 거미’ 인기2016.11.11
- 거미에 가까운 의미다. 거미집을 짓지 않고 모기 등 해충을 쫓아다니며 잡아먹는다. 보기에는 끔찍해도 해충을 잡아주니 인간에게는 친구인 셈이다. ※ 편집자주 세상에는 매일 신기하고 흥미로운 일이 많이 일어납니다. 보는 이의 눈살을 찌푸리게도 만들고, 감탄을 내뱉게 만들기도 하지요. ... ...

- IT는 장애인에 얼마나 친절한가2016.11.09
- 시작으로 최근 블로터까지 IT 분야만 팠다. 차에서 보내는 시간이 아까워서 들여다보기 시작한 노트북과 팜 파일럿 PDA는 순간이 아니라 인생을 바꿔 놓았다. 기술 하나에 일희일비하지 않고 역사와 흐름을 읽고자 한다. 세상은 늘 배울 게 많고, 기술은 거짓말하지 않는다고 생각한다 ... ...

- 사이비 종교에 빠지면 빠져나오지 못하는 이유2016.11.09
- 종교가 집단을 자기들만의 원칙 위에 결속시키기 위한 ‘핑계’에 지나지 않는다고 보기도 했다. 예컨대 축구를 할 때 사람들은 우르르 몰려다니며 공을 찬다. 하지만 축구의 핵심은 공이라기 보단 다양한 사람들이 특정 규칙 위에 모여 만드는 역동, 집단 활동에 있다. 축구를 종교와 비유하자면 ... ...

- 도시 속 ‘동물의 왕국’, 보닛 위의 매와 비둘기2016.11.07
- 그리고 자신의 차량 위에서 가장 ‘강렬한 야생의 질서’가 펼쳐지고 있었다. 평생 보기 힘든 장면이다. 사진은 놀라움과 함께 호기심도 자극하기 때문에, 지난주말 해외 네티즌들의 주목도가 높았다. ※ 편집자주 세상에는 매일 신기하고 흥미로운 일이 많이 일어납니다. 보는 이의 눈살을 ... ...

- [과학기자의 문화산책]달 기지 영상, 생중계 가능할까동아사이언스 l2016.11.06
- 98)’를 합쳐놓은 듯 보인다. 다소 무거운 주제지만 조석 작가 특유의 개그 감각이 더해져 보기 드문 코믹 SF 만화가 탄생했다. 그런데 이 웹툰을 보면서 드는 의문이 한 가지 있다. ‘문유’에서처럼 달 기지에서 촬영된 영상이 실시간으로 지구에 뿌려질 수 있을까. 통신 강도는 거리의 제곱에 ... ...
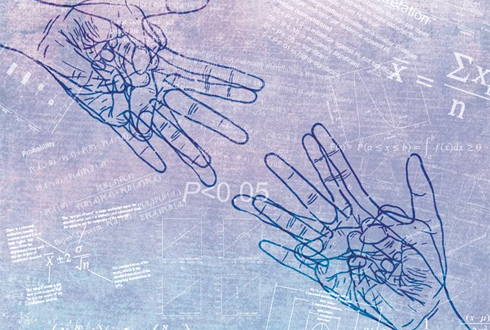
- 통계적 가설 검정과 입증의 책임 2016.11.06
- 귀무가설(null hypothesis)와 대립가설(alternative hypothesis)를 세웁니다. 귀무가설은 데이터를 보기 전에 상식적으로 여겨지는 가설이고 대립가설은 데이터를 통하여 입증하고자 하는 가설입니다. 여기서 p를 홍길동 씨의 가위바위보 게임의 승률로 정의하면 귀무가설은 p=0.5로 놓을 수 있고 대립가설은 p>0. ... ...
이전166167168169170171172173174 다음

















