뉴스
"개념"(으)로 총 2,825건 검색되었습니다.
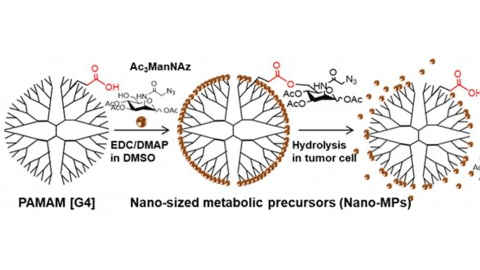
- 다양한 암세포 한 번에 잡는 신 개념 치료법 개발동아사이언스 l2017.10.17
- 연구진이 개발한 비천연당의 전달 모식도. - KIST 제공 몸속에 종양이 생기더라도, 종양을 구성하는 모든 세포의 성질이 동일하진 않다. 암세포가 저마다 서로 다른 특성을 갖기 때문이다. 이런 암세포의 이질성은 한 가지 약물로 암세포를 동시에 제거하기 어렵게 해 치료를 힘들게 만드는 원인이 ... ...

- 비정규직 연구원 “정규직 전환 가이드라인 늦어져 연구현장 혼란만”동아사이언스 l2017.10.17
- 동시에 연구를 하는 근로자인 학생연구원의 특수성을 고려한 새로운 노동자 개념이 필요하다”고 지적했다. 황윤정 연구원도 “일반적인 근로자와 같은 취급을 하게 되면 학업을 해야 하는 학생들에게 혼란을 줄 수 있고, 학생들의 연구 역량을 키워 줘야 할 연구자들에게도 방해가 될 수 있다”며 ... ...

- 경직된 국방 R&D, 미래 원천기술 확보에 주력해야… 출연연·대학 등 민간 협력이 관건동아사이언스 l2017.10.16
- Intelligence Digital X[trans]formation)’의 약어다. 육·공·해 통합 항만감시체계를 나타낸 개념도. - 국방과학연구소 제공 ● 국방硏 독점 체제로 폐쇄·경직된 국방 R&D… 책임·부담 등 연구자에게 불리한 요소도 개선돼야 그러나 이 같은 사례는 극히 제한적인 경우일 뿐, 대부분의 국방 R&D는 ... ...
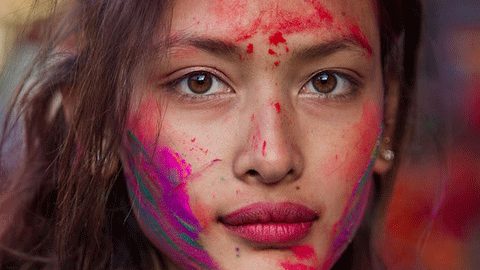
- 미녀란 무엇인가? ‘아름다움’을 다시 생각하게 하는 책팝뉴스 l2017.10.13
- 남아 있는 할머니나 불의의 사고로 한 쪽 다리를 잃은 장애인 여성 등 평소 미인이란 개념을 생각할 때 떠올리기 힘든 여성들도 많이 등장한다. 오늘날의 세계에서 사람들은 미인에 대한 일반적인 고정관념을 지니고 있고 그것이 소위 ‘표준’이 되지만, 그녀가 생각하기에 ‘미’란, “결국 ... ...

- 네이버 SW교육 ‘커넥트스쿨’ 초등 교육생 모집동아사이언스 l2017.10.13
- 만들고, 팀 프로젝트를 통해 함께 문제를 해결하는 시간을 갖는다. 소프트웨어의 기본 개념에서 프로젝트 설계 및 프로그래밍까지 체계적으로 배울 수 있다. 2017년 1학기 교육에 참여한 김준영 학생은 “직접 소프트웨어로 작품을 만들고 결과물이 뚝딱 나오는 것을 경험할 수 있어서 신기하고 ... ...

- 미녀란 무엇인가? 북한과 멕시코의 두 여성팝뉴스 l2017.10.13
- 꿈을 갖고 사는 다양한 직업 및 연령층 여성들의 사진은 묘한 감동을 준다. 미녀의 개념에 대해 다시 한 번 생각하게 만드는 책이라는 평가를 받는다. 사진 위는 멕시코 연방 경찰에서 헬리콥터 조종사 일을 하는 베레니체 토레스이다. 아기 엄마이기도 한 이 여성은 용감하다. 마약 갱단 소탕 ... ...

- 물웅덩이에 비친 평행 도시팝뉴스 l2017.10.12
- 개념이 있다. 현재 우리가 살고 있는 우주와 곁에 있는 또다른 우주들의 존재를 가정하는 개념이다. 사진 작가 귀도 구티에레스 루이스는 자신이 평행 도시의 모습을 촬영한다고 자평한다. ※ 편집자주 세상에는 매일 신기하고 흥미로운 일이 많이 일어납니다. 보는 이의 눈살을 찌푸리게도 ... ...

- [강석기의 과학카페] 2017 노벨상 발표를 지켜보며 떠오른 두 명의 로널드2017.10.10
- 영입해 1987년 라이고 프로젝트가 출범했다. 바이스는 부고에서 드레버가 라이고의 개념을 확립하는데 큰 기여를 했다고 인정하면서도 글 말미에 두 사람 사이가 얼마나 험악했는지를 짐작할 수 있는 에피소드를 들려줬다. 아무튼 한 사람은 평생의 염원인 중력파를 검출하는데 성공하는 모습을 본 ... ...

- 앨리스의 토끼 굴 속으로...앨리스展에서 인생샷 남겨보자!동아사이언스 l2017.10.05
- ” 속편 ‘거울나라의 앨리스’에서 앨리스가 만난 험프티 범프티는 비생일 개념에 대해 앨리스에게 설명한다. 1년 365일 중에 자신의 생일을 하루 뺀 나머지는 364일. 즉, 사람은 누구나 1년에 364일이 비생일(unbirthday)이다. 이번 전시에서는 영수증 기계에 생일을 입력하면, 마치 포춘쿠키나 오늘의 ... ...

- 수학을 사랑한 판화가 에셔...이번 연휴에 아이랑 만나보자동아사이언스 l2017.10.04
- 조지 폴리아의 ‘평면 대칭군’에 관한 논문을 읽고, 17개의 평면 대칭군 개념을 이해하게 된다. 그 결과 ‘평면을 규칙적으로 나눠 공간을 채우는’ 자신만의 테셀레이션을 완성한다. 이번 전시에서는 특별히 그의 테셀레이션 작품 중 가장 유명한 ‘도마뱀’과 관련된 포토존이 마련돼 있다. ... ...
이전192193194195196197198199200 다음