추천검색어
기수
뉴스
"홀수"(으)로 총 27건 검색되었습니다.
- [주말N수학] 과학계가 3월14일을 기념하는 이유수학동아 2021.03.13
- 고드프리트 라이프니츠가 고안한 원주율 계산식. 이 식의 우변은 1과 1/3, 1/5처럼 분모가 홀수고 분자가 1인 분수를 순서대로 더하고 빼는 과정을 무한히 반복한다는 의미다. 하지만 이 방식으로는 300번째 항까지 계산해도 원주율이 소수점 아래 2번째 자릿수까지만 정확하게 나온다는 한계가 있다. ... ...

- [주말N수학] 196883 차원의 대칭 괴물2020.10.24
- 숫자를 규명한 것이다. 우리 생활에서 흔히 접하는 수는 자연수다. 자연수에는 짝수, 홀수, 삼각수, 완전수 등 다양한 수가 있다. 그중에서 가장 중요한 자연수의 모임을 고르라면, 모든 수학자가 아마 ‘소수’라고 외치지 않을까 싶다. 1과 자신만을 약수로 갖는 소수는 모든 수를 이루는 기본 ... ...

- [주말N수학] 삼각형으로 둘러싸인 n차원 구 문제2019.02.16
- n차원에서도 비슷한 방식으로 단체 구를 만들면 f0-f1+f2-f3+…+(-1)n-1fn-1 의 값이 n이 홀수면 2, n이 짝수면 0입니다. 프랑스 수학자 앙리 푸앵카레가 대수적 위상수학 방법을 써서 이걸 증명했습니다. 이처럼 단체 구에서 얻을 수 있는 f 값들은 특정 수로 정해져 있습니다. 이 f 값들을 모은 (f0, f1, f2, … ... ...

- [주말N수학] 새로운 도형의 등장 '뫼비우스 칼레이도사이클'수학동아 2019.02.02
- 짝수 개의 사면체로만 만들 수 있었다. 반면, 뫼비우스 칼레이도사이클은 홀수와 짝수에 상관없이 사면체를 연결해 만들 수 있었습니다. 또 절대 도형이 흐트러지지 않았습니다. 사면체 개수를 늘리면 3번 꼬인 뫼비우스 띠가 나타나는 뫼비우스 칼레이도사이클. 엘리엇 프라이드, PNAS 제공 ... ...

- 유대인 강제수용소에서 탄생한 '벽돌공장 문제'2018.10.09
- 홀수인지 짝수인지 결정하는 것조차 NP-난해라는 것을 밝혔습니다. 즉 최소 교차점 수가 홀수인지 다항식 시간에 알 수 있다면 P=NP가 돼, 다른 어려운 모든 NP-난해 문제도 모두 다항식 시간에 해결할 수 있게 되는 것이죠. 심지어 임의의 소수 에 대해 최소 교차점 수가 p의 배수인지 결정하는 문제 ... ...

- 놀이야? 체험으로 배우는 수학이야! '수와북 연구소'수학동아 2018.10.08
- 체험을 하고 있군요. 달리는 차에 앉아 짝수만 골라잡는 게임입니다. 눈앞에 수가 모두 홀수라면 양손을 들어올려 피해야 하지요.이번에는 게임 속 주인공이 됐습니다. 악당을 물리치며 떠나는 모험에 나오는 수학 문제를 해결해야 합니다. 문제를 해결하지 못하면 다음 단계로 넘어갈 수 ... ...
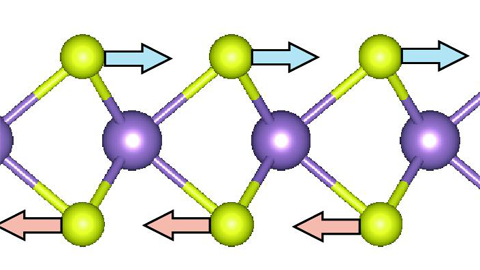
- 원자 춤추게 하면 자성없던 물질도 자석으로 변신동아사이언스 2018.02.28
- 때문에 발생하는 힘이 평형을 이룬다. 따라서 짝수 전자로는 자성을 만들기 어렵고, 홀수 전자를 가진 금속 원자만이 자성을 만들 수 있었다. 철, 니켈, 코발트 정도가 자석을 만들 수 있는 금속이었다. 연구팀이 개발한 기술을 이용하면 그동안 자석을 만들 수 없었던 물질로도 자석을 만들 수있다. ... ...
- 수학의 변신은 무죄! 예술이 된 난제수학동아 2017.08.30
- 1937년 독일 수학자 로타르 콜라츠가 제시한 문제로, 어떤 자연수든지 짝수면 2로 나누고 홀수면 3을 곱한 뒤 1을 더하다 보면 결국 1이 된다는 추측이에요. 예를 들어 3은 7번(3→10→5→16→8→4→2→1)만에 1이 되지요. 간단한 것 같지만 27은 무려 111번을 반복해야 1이 돼요. 벨로스는 수학예술가 ... ...

- [강석기의 과학카페] 나무로 지은 아파트에서 사는 시대 올까?2017.05.30
- 구조용집성판(CLT)의 등장으로 나무로 고층 건물을 지을 수 있게 됐다. 보통 널빤지를 홀수 개 붙이는데 바깥쪽 판의 나뭇결을 길이 방향으로 맞추기 위해서다. - 위키피디아 제공 한편 화재의 경우도 나무가 철이나 콘크리트보다 오히려 안전하다고 한다. 즉 불이 어느 수준을 넘으면 철이 녹고 ... ...

- 시에르핀스키 문제 이제 다섯 걸음 남았다수학동아 2017.01.13
- n을 대입해 k·2n+1을 계산한 값이 소수라는 것을 보이면 되는 것이지요. 78557보다 작은 홀수는 3만 9278개나 있지만 대부분이 n이 9이하의 자연수일 때 k·2n+1의 값이 소수라고 밝혀져 가장 작은 시에르핀스키 수의 후보는 얼마 전까지 6개였습니다. 그런데 2016년 10월 31일 페테르가 10223마저 시에르핀스키 ... ...







