뉴스
"가정"(으)로 총 2,444건 검색되었습니다.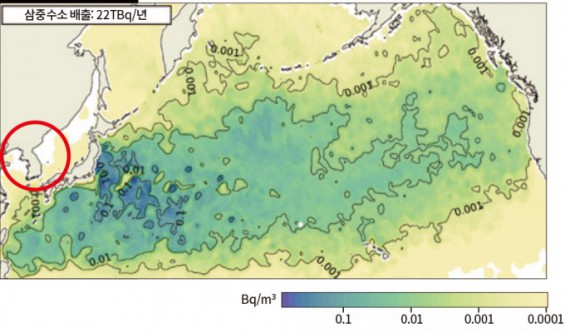
- [日 오염수 팩트체크] ④일본이 방출한다는 삼중수소 양, 문제없다?과학동아 2023.07.12
- 삼중수소 농도를 예측했다. 연구팀은 일본이 삼중수소를 22TBq씩 10년간 방출한다는 가정 아래 오염수가 해양에서 어떻게 확산되는지 알아봤다. 오염수는 북태평양 전체로 퍼졌으며 아열대 소용돌이에 갇혔다. 그 중 일부가 쿠로시오 해류와 대마 난류를 타고 제주도 남동쪽으로 들어와 동해로 흘러 ... ...

- "해산물 수입 금지 조치 유지… 대비책은 '최악의 시나리오' 가정한 것"동아사이언스 2023.07.07
- K4 탱크에 모여 있는 오염수가 한번에 쏟아져 나올 경우를 '최악의 시나리오'라고 가정하고 대비책을 수립한 것으로 알고 있다." Q. 향후 해산물을 어떻게 감시하고 관리할 것인지. "후쿠시마 오염수 방류 후 3개월 동안 집중적으로 관리할 계획이다. 관리 장비에 대해선 가까운 시일 내에 ... ...
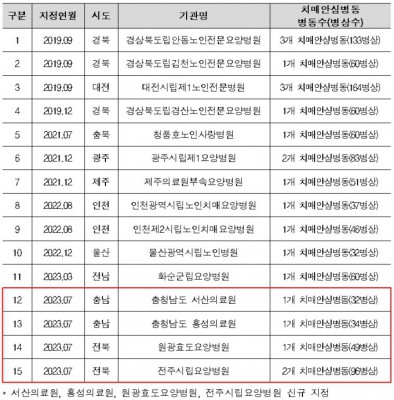
- 치매안심병원 4곳 추가 지정...민간요양병원 첫 포함동아사이언스 2023.07.04
- 치매안심병원이 되면 ‘치매안심병동 인센티브 시범사업’에 참여할 수 있다. 이 사업은 가정에서 돌보기 어려운 치매 환자(행동심리, 섬망 증상 등)를 집중치료해 지역사회로 복귀토록 한 성과를 평가해 수가를 지급하는 시범사업이다. 입원 1일당 치매안심병동 4만 5000원, 치매안심병원 6만1000원 ... ...

- [일상 속 뇌과학] 뇌의 '회춘' 위한 새 단서 찾았다2023.06.30
- 이를 피하기 위해서다. 인간의 노화를 극복하기 위한 ‘무엇’인가를 개발하고 싶다고 가정하자. 그렇다면 사람의 노화가 어떻게 시작되고 진행되는지 그리고 그에 따른 문제점들을 파헤치는 것에서 연구는 시작될 것이다. 하지만 실제로 그 열망을 현실로 옮기기 위해 노인의 앞에 서게 된다면 ... ...

- 미국서 20년 만에 말라리아 환자 발생...국내서도 꾸준히 늘어동아사이언스 2023.06.28
- 미국에서 20년 만에 연달아 5명의 말라리아 확진 환자가 발생했다. 사진=tskstock/게티이미지 미국에서 20년 만에 말라리아 환자들이 연이어 발생했다. ... 플로리다와 텍사스 주 정부는 말라리아 예방을 위해 바깥활동 시 긴소매를 착용하고, 가정 내 방충망 상태를 점검할 것을 요청하고 있다. ... ...

- 오염수 방류 임박...정부 “식품 방사선 기준, 세계 어느나라보다 엄격”동아사이언스 2023.06.26
- 개정했다”며 “우리 국민이 섭취하는 식품의 절반인 50%가 방사능에 오염됐다고 가정해 매우 보수적으로 기준을 강화한 것”이라며 “강화된 기준을 적용했을 때도 연간 세슘 방사선 노출량은 0.44mSv로 최대 안전 기준의 절반이 안되는 수준”이라고 덧붙였다. ... ...

- 미국국가정보국 "코로나19 우한실험실 유출 증거 찾지 못해“동아사이언스 2023.06.25
- 9 바이러스가 자연환경에서 유출됐다는 가설과 실험실에서 유출됐다는 가설 모두 가정에 의존하거나, 가설과 상반된 보고가 있다”며 “코로나19 대유행의 정확한 기원을 파악할 수 없었다”고 밝혔다. 실험실 유출 가설과 관련해 우한바이러스연구소에서 코로나19 바이러스에 대한 광범위한 ... ...

- [주말N수학] 수학자에서 사회운동가로...러셀의 삶을 뒤흔든 역설수학동아 2023.06.24
- 문제는 다음과 같습니다. R은 자기 자신을 포함할까요? R이 자기 자신을 포함한다고 가정해볼게요. R의 정의에 따라 R은 자기 자신을 포함하지 않습니다. 이것은 모순이네요. 따라서 R은 자기 자신을 포함할 수 없습니다. 그러나 R은 자기 자신을 포함하지 않는 모든 집합을 포함하므로 R은 자기 ... ...

- [주말N수학] 2000년 동안 서구 문명 지배한 '유클리드 기하학'수학동아 2023.06.17
- 9세기 수학자들은 평행선 공준을 그대로 증명하기 어렵다고 판단하고 명제를 거짓이라고 가정할 때 생기는 모순을 보여 역으로 명제를 증명하는 ‘귀류법’을 활용하기로 했습니다. 그런데 평행선 공준을 거짓이라고 생각해도 전혀 기하학에 모순이 생기지 않았어요. 당시 수학자들은 평행선 ... ...

- 화재위험 낮은 전고체 전지 상용화 이끌 전해질 공정 개발동아사이언스 2023.06.06
- 활용하면 고순도 고체 전해질 생산이 가능하다. 특히 마이크로파 합성공정은 가정용으로 쓰이는 2.45기가헤르츠의 전자기파 형태로 전기에너지를 직접 반응물에 쬔다. 이 경우 에너지 변환 과정에서 발생하는 전력 손실량을 줄일 수 있어 비용 절감과 에너지 효율화가 가능하다. 김동완 ... ...







