뉴스
"어떤 특정한 때"(으)로 총 1,083건 검색되었습니다.
- 노태문 삼성전자 사장 "혁신으로 모바일 업계 동반성장 이끌 것"연합뉴스 2020.02.13
- 삼성이 업계 선두가 아닌 후발 주자였고 스마트폰에 처음 뛰어들 때도 어려웠다는 점을 상기시켰다. 노 사장은 그럼에도 "우리에겐 한계를 ... 제품은 계속 개발 중이지만 완성도가 확보돼야 공개할 수 있다"며 "지금 어떤 형태의 제품이라고 말하긴 어렵고 다양한 여러 가지를 물밑에서 많이 하고 ... ...
- 차별이 통증보다 아프다동아사이언스 2020.02.10
- 뜻으로 풀이된다. 연구팀은 기능적 자기공명영상(fMRI) 장치로 뇌의 어떤 부분이 이런 차이를 만드는지도 살펴봤다. 흑인 참가자들에게서만 차별을 당한 횟수가 많을수록 열 통증을 가했을 때 뇌의 측좌핵(NAc) 영역이 다른 영역보다 더 많은 신호를 내는 것으로 나타났다. 우 교수는 ... ...

- [프리미엄 리포트] 총천연색 차세대 발광 소자, 퀀텀닷과학동아 2020.02.08
- 입자 표면이 퀀텀닷 전체의 특성을 결정짓는데 중요한 역할을 한다. 이 때문에 퀀텀닷은 중심 물질(핵)을 껍질(쉘)로 싸고, 껍질에 다시 추가로 ... 않고 제 기능을 할 수 있도록 만든다. 배 교수는 “어떤 종류의 리간드를 어떤 구조로 부착하는지가 퀀텀닷의 기능에 매우 중요하다”며 “리간드뿐만 ... ...

- [사이언스N사피엔스]과학혁명의 배경2020.02.06
- 출현시킨 요인으로 르네상스, 종교개혁, 과학혁명을 꼽는 이들도 있다. 어떤 기준을 적용하든 과학혁명이 인류의 역사에서 지대한 변곡점을 ... 아니다. 시기적으로도 16세기에 접어들면 르네상스도 막바지로 치달을 때이다. 루터의 종교개혁이 시작된 지 10년 뒤인 1527년에는 신성로마제국군이 ... ...

- "2번 환자 치료한 에이즈약 부작용 가능성" 안전한 치료제 개발에 AI도 뛴다동아사이언스 2020.02.05
- 제안했다. 홍콩과기대 연구팀은 신종 코로나바이러스 백신을 개발할 때 어떤 것을 표적으로 삼으면 좋을지 제안하는 연구결과를 내놓기도 했다. 연구팀은 신종 코로나바이러스의 유전정보를 이용해 바이러스 표면에 난 단백질들의 3차원 구조를 모델링했다. 그 결과 B세포와 T세포 등 면역세포가 ... ...

- [강석기의 과학카페] 아픈 자, 죽는 자, 멀쩡한 자2020.02.04
- 모든 숙주에게 통하는 건 아니다. 숙주의 유전적 다양성이 크기 때문이다. 어떤 단계에서 바이러스에 취약한 유전형을 지닌 불행한 숙주는 심각한 증상을 겪을 수 있지만 특정 단계의 진행을 방해하는 유전형을 지닌 숙주는 감염 자체가 되지 않거나 감염이 돼도 증식이 잘 안 돼 무증상 또는 경미한 ... ...
- 의사들도 헷갈리는 신종코로나의 5가지 궁금증연합뉴스 2020.02.04
- 두 번째는 신종 코로나바이러스의 확진 진단은 어떤 식으로 하는 것인가 하는 점입니다. 신종 ... 감염내과 이은영 교수는 "바이러스에 있는 특정한 유전자의 조각을 확인하는 방법"이라며 ... 고 설명했습니다. 세 번째는 일반인이 대화할 때 마스크를 착용한 채 얘기하는 것은 과한 것인가 하는 ... ...
- '신종 코로나바이러스' 감염여부 6시간이면 알 수 있다동아사이언스 2020.01.31
- 해독을 거쳐 중국에서 발표한 바이러스 유전자와 비교하는 식으로 어떤 종류인지 판단했다. 분석에 하루가 걸릴 뿐 아니라 여러 검체의 분석을 ... 형광을 내는 물질과 형광을 막는 물질이 붙어있는데 서로 붙어있을 때는 빛이 나지 않는다. 하지만 PCR을 통해 코로나바이러스의 특정 염기서열이 ... ...
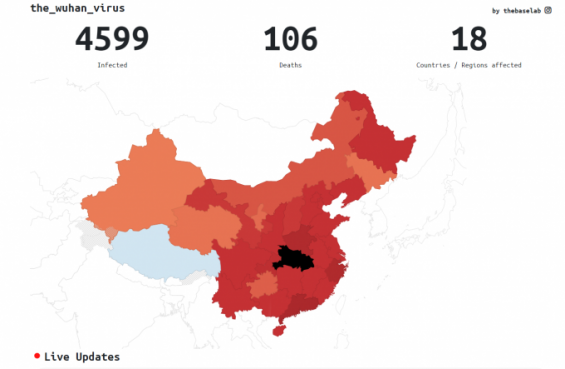
- [팩트체크]"환자 갔던 카페 안전할까" 신종 코로나바이러스 루머들동아사이언스 2020.01.28
- 있었던 것만으로 감염될 확률은 매우 낮을 것”이라고 말했다. 어떤 이들은 중국으로부터 주문한 공산품과 특히 식료품이 신종 ... 체내에 들어가 감염시킨다. 근거리(1~2m 이내)에 있던 환자가 기침을 했을 때 튀어나오는 미세한 침방울이 다른 사람의 호흡기로 들어가 침방울 안에 있던 ... ...

- [프리미엄 리포트] 한국 로봇 개발의 현장에 가다과학동아 2020.01.26
- ‘변신 기능’을 추가한 것이다. 오 교수는 “휴머노이드가 움직일 때 관절마다 위치와 속도, 가속도가 모두 다르다”며 “어떤 조합이 가장 이상적인지, 어떤 조합이 에너지를 최소화하는지 수억 개의 조합을 계산해 그중 최선의 조합을 제시해야 로봇이 움직일 수 있다”고 설명했다. 그는 ... ...








