뉴스
"도형"(으)로 총 167건 검색되었습니다.
- [표지로 읽는 과학] 더 강하고 가벼운 금속재료를 만드는 법동아사이언스 l2021.09.19
- 제공 국제학술지 ‘사이언스’는 17일 불규칙적인 형태를 가진 형형색색의 도형이 서로 연결돼 있는 모습을 표지로 실었다. 금속산화물을 녹여 붙이거나 표면에 안료를 구워서 붙인 색판 유리조각을 접합시켜 유리창으로 쓰는 스테인드글라스처럼 보이기도 한다. 이 사진의 정체는 적외선으로 ... ...
- [주말N수학]원리를 꿰뚫는 수학 공부법을 찾아라수학동아 l2021.08.28
- 적분이라는 수학 개념으로 연결돼 있다는 겁니다. 현재 교육과정에서 구와 같은 입체 도형의 성질과 부피 공식은 중학교 1~2학년 때 배우며, 미분과 적분의 개념은 고등학교 때 배우고 있는데요. 조 대표는 “미분과 적분으로 관통할 수 있는 문제를 따로 배우는 것으로 볼 수 있다”며 “수학을 ... ...
- [표지로 읽는 과학]경이로운 기하학적 형태를 띠는 꽃의 비밀동아사이언스 l2021.07.11
- 식물 기관이 발달하는 동안 분열 조직이 제기능을 했다면 지금과 같은 차원 분열 형태의 도형이 아닌 원뿔 구조의 꽃이 만들어졌을 것이라는 분석이다. 연구팀은 “식물 발달 전반에 걸쳐 분열 조직은 정형화된 형태로 나선 또는 소용돌이 형태로 기관을 생성하는데 콜리플라워는 다수의 나선이 ... ...
- [주말N수학] 수학과 문학의 수상한 만남, 시인 함기석수학동아 l2021.06.19
- 말합니다. 전혀 다른 도형으로 여겨지는 정육면체와 구를 위상 수학에서는 똑같은 도형으로 보듯, 어떤 관점을 가지는지에 따라 사람도 세상도 전혀 다르게 볼 수 있다는 것을 깨달았다고 합니다. 함 작가는 “기하학을 통해 세상을 다르게 보게 된 것처럼, 수학으로 세상을 관찰하면 색다른 세상을 ... ...
- [인터뷰]상상의 학문, 그리고 도구나 논리가 아닌, 실체가 있는 수학의 세계 수학동아 l2021.06.12
- 표현되는 공간을 연구하는 분야입니다. 대수기하학은 대수적 방정식들로 정의될 수 있는 도형을 연구하는 분야입니다. 황 단장은 1999년 기하학 분야에서 한동안 풀리지 않았던 공간 사이의 변환에 관한 난제인 '라자스펠트 예상'을 증명한 데 이어 40여 년간 미해결 문제로 남아 있던 변형불변성 ... ...
- [주말N수학] 수학계를 주름잡는 수학 명가수학동아 l2021.05.08
- 김영욱 고려대학교 수학과 명예교수 Q. 교수님의 가족을 소개해달라. 저는 곡면과 같은 도형의 성질을 미분 개념을 이용해 이해하는 미분 기하학을 연구했습니다. 제 아버지인 김치영 수학자는 해방 후 1세대 수학자로 연세대 수학과를 비롯한 많은 대학에서 수학을 가르쳤습니다. 우리나라에서 ... ...
- [인터뷰] 백남준의 꿈에 전기를 수혈한 장인과학동아 l2021.05.01
- 그려진 작품의 설계도를 보여줬다. 설계도라기보단 낙서에 가까운 그림이었다. 그는 도형과 한자, 한글이 뒤섞여 있는 설계도를 찬찬히 풀이해줬다. “제품명은 ‘도너츠’. 이쪽엔 30~60W(와트)가 필요하고 코일은 300번 정도 감으면 될 것 같다…. 이런 내용이 써 있어요. 암호처럼 써 있어서 아마 ... ...
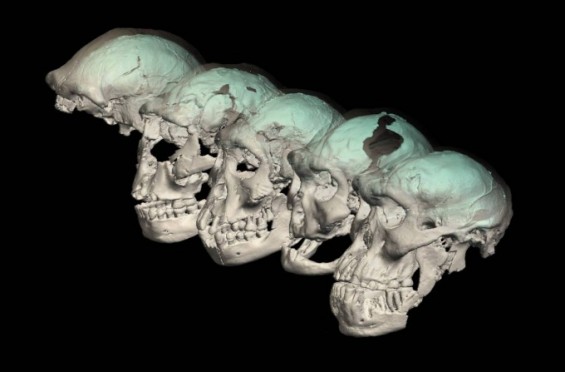
- [강석기의 과학카페] 호모 에렉투스, 사건의 재구성2021.04.27
- 호모 날레디로, 뇌가 무척 작고 원시적임을 알 수 있다. 점선은 아이의 뇌이고 속이 빈 도형은 해상력이 떨어져 유형 확인에 실패한 시료다. 가로축은 시간(단위: 100만 년 전)이고 세로축은 뇌용량이다. 사이언스 제공 ○ 아시아 호모 에렉투스의 조상 아냐 분석 결과 드마니시인 다섯 명의 뇌는 ... ...
- [주말N수학] 펜로즈 타일과 대칭2021.04.24
- 반복된다. 위키미디어 제공 펜로즈 타일에서 시작된 노벨 화학상 그렇다면 같은 모양의 도형을 사용해서 대칭적으로 반복되는 기본 패턴 없이 평면을 무한하게 채워나가는 것은 가능할까? 얼핏 불가능한 일처럼 생각된다. 하지만 그 어려운 일을 해낸 사람이 있다. 바로 펜로즈 명예교수다. 그는 ... ...
- [주말N수학] 엉덩이는 한 개인가, 두 개인가수학동아 l2021.04.10
- 다른 도형이다. 그럼 이 개념을 엉덩이에 한 번 적용해보면 위상수학으로 보면 도형의 모서리나 움푹 들어간 부분처럼 크게 꺾인 부분은 모두 둥글어질 수 있다. 따라서 엉덩이에 공기를 넣는다고 생각하면 엉덩이의 두 짝을 나누던 모서리 역시 둥글어지고, 한 개의 덩이만 남는다. 따라서 ... ...
이전123456789 다음
