뉴스
"존재"(으)로 총 6,354건 검색되었습니다.

- 중국發 초미세먼지는 중금속 덩어리동아사이언스 l2014.02.12
- 책임연구원팀은 대전 지역에서 채취한 초미세먼지를 분석해 중금속 원소들의 화학적 존재형태 및 함량을 확인했다. 채취된 초미세먼지의 평균 중금속 함량은 카드뮴 44ppm(1ppm=100만분의 1), 비소 290ppm, 납 2520ppm, 아연 5490ppm 등으로 나타났다. 연구팀에 따르면 호흡기를 통해 초미세먼지가 ... ...

- [에디터 칼럼] 황우석과 씻김굿동아사이언스 l2014.02.12
- 사면 배가 아프다’는 말이 있을 정도로 피붙이가 잘 되도 질투가 나고, 과거를 후회하는 존재가 사람이다. 이웃 일본은 줄기세포로 노벨과학상을 수상하고, 새로운 기술을 만들어내고 있으며, 미국과 유럽에서도 다양한 연구성과를 내고 있다는 소식은 들리는데, 우리나라의 줄기세포 연구는 ... ...

- 황우석 1번 배아줄기세포 미국서 특허 인증…관련주 급등동아일보 l2014.02.12
- 교수팀이 체세포 복제 방식으로 만들었다고 발표했던 배아줄기세포 중 유일하게 실제로 존재하는 것이다. 다만, 이번 특허 등록으로 NT-1이 체세포 복제가 성공해서 만들어진 줄기세포라는 황 전 교수측의 주장이 과학적으로 확인된 것은 아니다. 특허 심사는 서류상으로만 이뤄질 뿐 실제 실험으로 ... ...
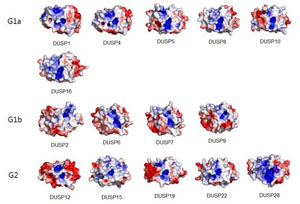
- 암·뇌졸중 원인 단백질 구조 기능 밝혔다동아사이언스 l2014.02.11
- 구조적 차이에 따라 각각 선택적으로 반응한다는 사실을 밝혀냈다. 이를 통해 DUSP에 존재하는 효소활성 부위의 표면과 전하 배치 등 각각의 특징을 규명하는 데 성공했다. 류성언 교수는 “백혈병 선택 치료제 ‘글리벡’처럼 이번에 밝혀낸 DUSP의 구조를 이용해 다른 난치병들도 효과적으로 ... ...

- ‘나’도 모르는 내 마음, ‘뇌’는 알고 있다동아사이언스 l2014.02.09
- 연구가 상세히 소개돼 있다. 한때 각 기능에 부합하는 뇌의 특정 영역이 존재한다는 생각이 뇌 과학의 주류를 이뤘지만, 최근 신경과학에서는 어긋나는 증거가 늘고 있다. 특정 인지 기능이 대뇌 피질의 특정 세포 조직에 모여 있지 않고 피질 속에 널리 분산된 그물망에서 작동한다는 것이다. ... ...

- 수분, 피부가 아니라 열대우림에 양보하세요동아사이언스 l2014.02.09
- 증가했고, 산불 횟수도 적었다는 것. 브라질 핵에너지연구소 가티 박사는 “수분의 존재 여부에 따라 아마존은 탄소 흡입구가 될 수도 있고, 배출구가 될 수도 있다는 것을 보여준 연구 결과”며 “이번 연구로 토지 이용을 위해 인위적으로 밀림에 불을 지르는 행위가 지구 건강에 얼마나 ... ...

- 수학을 좋아한다면 이런 직업 어떨까요?수학동아 l2014.02.05
- 위키미디어 제공 수학을 좋아하는 사람들에게 최고의 만족을 줄 수 있는 직업은 무엇일까? 최근 미국 경 ... 순서로 나열할 때 가장 중앙에 위치하는 값을 의미한다. 연봉과 같이 월등히 높거나 낮은 값이 존재할 때는 중앙값을 주로 사용한다 ... ...

- 가족사랑, 지구사랑탐사대로 확인하세요!어린이과학동아 l2014.02.03
- 만지고 잡는 데 거리낌이 없다. 자연 속에서 탐사를 하며 동식물들과 친해지고 친구같은 존재로 생각하기 때문이다. 때문에 탐사대원 어린이들은 밝고 학교에서 친구들과도 사이가 좋은 것으로 나타났다. - (주)동아사이언스 제공 마지막으로 탐사대원인 어린이들이 이공계 관련 진로 멘토링을 받을 ... ...

- ‘겨울왕국’ 얼음여왕 엘사의 비밀동아사이언스 l2014.01.29
- 투명하고 유동성이 좋은 액체질소의 끓는점은 약 영하196도. 공기 중에 질소가 70% 이상 존재하고, 액체헬륨 같은 다른 냉매보다 ‘기화열’이 크기 때문에 경제적이고 냉각능력도 좋다. 액체질소는 얼리려는 물체의 열을 빼앗아 기체가 되는데, 이 때 물체로부터 많은 열을 빼앗아도 기체로 상태가 ... ...

- "'돼지꿈' 만들어 드립니다~."과학동아 l2014.01.29
- 영화 ‘인셉션’은 꿈을 조절할 수 있는 설정으로 화제가 됐다. 그런 기계가 실제로 존재한다면 어떨까. 영국 일간지 데일리메일은 1월 16일, 잠을 자는 동안 꿈을 현실처럼 인식하고 조절할 수 있게 하는 머리 밴드가 개발됐다고 보도했다. 납작한 전자장치가 부착된 ‘오로라 스마트 ... ...
이전606607608609610611612613614 다음

















