뉴스
"이야기"(으)로 총 4,726건 검색되었습니다.

- 예상보다 더 빠른 '지구온난화'..."가까운 미래에 1.5도 상승"동아사이언스 l2023.03.21
- 복잡해지고 연쇄적으로 발생할 것이라 분석했다. 지금보다 대응이 더 어려워질 것이란 이야기다. 이러한 이유로 실행 가능하고 효율적인 적응대책이 시급하다고 강조했다. 기후 온난화의 향후 양상에 따라 효율이 낮거나 제약이 따르는 대책이 있을 수 있지만, 장기적인 계획을 수립하고 이행해 ... ...

- [박정연의 닥터스] “몸도 기억하는 트라우마...신체로 치료해요"동아사이언스 l2023.03.20
- 생각한다. 섣불리 다 안다는 듯한 태도를 취하거나, 왜 극복하지 못하느냐, 아직도 그 이야기를 하느냐고 쉽게 말해서는 안된다고 본다. 이러한 의미에서 우리 사회에서 트라우마 피해자를 대하는 태도는 무척 안타깝다. 통계에 의하면 인구의 절반 이상이 일생 동안 살아가면서 적어도 한번 ... ...

- [과학게시판] KIST·수림문화재단, '과학을 바라보는 예술가의 시선' 전시 동아사이언스 l2023.03.18
- 새롭게 발견해야 할 '인간성', 인간에 의해 범주화된 프레임이 만들어낸 '자연성'에 대해 이야기한다. KIST 과학자들과 예술가들이 함께 창작한 5개의 작품을 비롯해 총 8개의 작품이 전시된다 ... ...

- [오늘과학] "아이의 외국어 습득, 성인보다 또래와 대화가 더 중요"동아사이언스 l2023.03.14
- 아이들은 북미 국가에서 외국어 교육을 받은 아이들보다 2~4배 긴 시간 다른 언어로 이야기를 했다. 연구팀은 "말라쿨라섬 아이들의 다국어 습득 사례를 미뤄보았을 때 아이들의 언어 습득과정에선 부모의 역할만큼 또래 아이들과의 교류가 중요하다"고 말했다. 다만 이번 연구가 모든 보편적인 ... ...

- [의학사로 보는 세상] 18세기 말 키 2.3미터 거구 시체의 해부2023.03.14
- 보여주기도 했다. 헌터 형제는 어떻게 수많은 해부용 시체를 얻을 수 있었을까. 한마디로 이야기하자면 훔쳐 오는 것이었다. 사회적 지위도 있고, 다른 일을 하기에도 바빴으므로 직접 훔쳐온 것이 아니라 시체를 공급해 줄 이들과 계약을 맺고, 공급업자들이 세상을 떠난지 얼마되지 않은 빈민의 ... ...

- [프리미엄리포트] 고열 견디는 합금, 에너지 위기 해결에 일조할까과학동아 l2023.03.11
- 구부러지는 이유는 가열한 철처럼 열역학적 상대온도가 높기 때문이다. 하지만 이번 이야기의 주인공인 니켈은 이런 규칙을 깬다. 니켈은 용융점이 1728K(1455℃)으로 철보다 낮지만 니켈을 기본으로 만든 합금은 높은 온도에서도 강도를 유지한다. 비밀은 아름다운 미세조직에 있다. 니켈-크롬 ... ...

- [박진영의 사회심리학] 타인의 시선에서 생각하기 능력의 중요성2023.03.11
- 사랑 없이는 살아갈 수 없는 인간이라는 동물은 분명 사랑하기 위해서 존재한다는 이야기였다. 이런 관점에서 볼 때 이해하기 위한 노력을 멈추는 것은 사랑하기를 멈추는 것과 같을지도 모르겠다. 사랑하기를 멈춘다면 내 존재 이유 또한 멈추는 것이 아닐까. 이해하기를 멈추지 말아야 겠다. ... ...
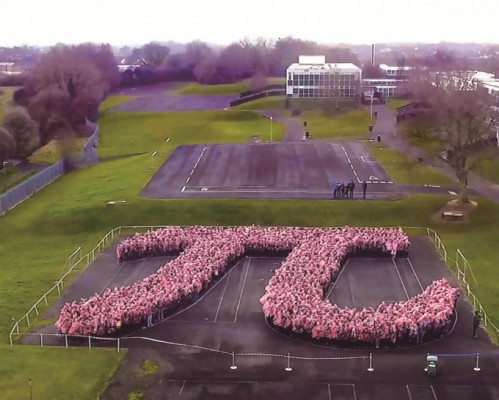
- [주말N수학] 원주율에 '진심'인 사람들...소수점 100조 자리까지 계산수학동아 l2023.03.11
- 원주율을 7만 자리까지 외워 기네스 세계 기록에 오른 인도의 라즈비르 미나의 이야기를 들어봤습니다. 중동 지역 국가인 오만에 있는 술탄학교에서 사람으로 원주율을 가장 길게 표현한 세계 기록을 가지고 있어요. 2018년 π-데이를 기념하기 위해 모든 학생과 전직원, 그리고 학부모까지 손에 ... ...
- [강석기의 과학카페] 불안감과 두근거림 어느쪽이 먼저일까2023.03.08
- 게티이미지뱅크 제공 ‘어 가슴이 왜 이렇게 두근거리지?’ 카페인에 민감한 편이라 커피를 아침, 점심 두 잔만 마시는데 그날은 오후 서너 시에 한 잔 ... 과학카페》(1~7권),《생명과학의 기원을 찾아서》가 있다. 번역서로는 《반물질》, 《가슴이야기》, 《프루프: 술의 과학》을 썼다 ... ...

- [주말N수학] 허수 i는 필요한 이유수학동아 l2023.03.04
- 실수 계수를 가진 방정식도 마찬가지로 모든 해가 실수는 아니지요. 하지만 앞서 이야기한 가우스의 대수학의 기본 정리에 의해 모든 복소수 계수를 가진 복소수 방정식의 해는 언제나 복소수예요. 그러니까 수 체계를 더 확장할 걱정이 없어요. 방정식의 해를 표현하기 위해 더 큰 차원의 수가 ... ...
이전616263646566676869 다음