뉴스
"둘"(으)로 총 2,015건 검색되었습니다.

- [이강운의 곤충記] 곤충 날개의 등장은 필승 전략이었다2019.03.06
- 곤충이 2쌍의 날개를 가지고 있으나 파리목은 2개의 날개만 가지고 있다. 'Diptera'의 'Di'는 둘, 즉 2개의 날개를 가지고 있다는 뜻으로 뒷날개 한 쌍을 몸의 균형을 유지하는 평균곤(halter)으로 과감히 변형하여 단순화 시키는 진화를 택했다. 물론 날개가 2개인 모기나 각다귀도 파리목에 속한다. ... ...

- [내 마음은 왜 이럴까?] 신생아 황달 생기는 진화적 이유2019.03.03
- 인류는 긴 세월 동안 둘 사이의 아슬아슬한 줄타기를 하면서 생존해왔습니다. 에필로그 대개 고빌리루빈혈증이나 신생아 황달은 금세 좋아집니다. 약간 황달기가 있다고 해도 너무 걱정할 것은 없습니다. 열심히 항산화 기능을 수행하고 있다는 의미일 수도 있으니까요 ... ...

- 임신중 '반일란성 쌍둥이' 첫 발견동아사이언스 l2019.02.28
- 쌍둥이(semi-identical)라 부르는 일란성도 이란성도 아닌 쌍둥이다. 공동 1등을 차지한 정자 둘이 만들어낸 결과다. 마이클 가벳 호주 퀸즐랜드공대 생의학과학부 연구원 연구팀은 세계에서 두 번째로, 임신 중엔 첫 번째로 반일란성 쌍둥이를 호주 브리즈번에서 발견했다고 이달 28일 국제학술지 ... ...

- [3·1운동 100주년]"대한의 모든 존재에게 한글 이름을 허하라"과학동아 l2019.02.28
- 통해 현실을 극복하고자 노력했던 연구자들이 있었다. 바로 조복성과 김병하다. 이 둘은 모두 박물학을 통해 대중을 일깨워야 한다는 사명감을 갖고 있었다. 조복성은 평양고등보통학교와 연희전문학교를 졸업한 뒤 보통학교 교사를 거쳐 경성제국대학 예과 연구원으로 활동한 인물로, 1929년 ... ...

- 버려지는 글리세롤로 수소와 화학원료 생산 기술 개발동아사이언스 l2019.02.27
- 보일 수 있도록 했다. 그래파이트와 그래핀 둘 다 탄소의 동소체 중 하나이다. 하지만 둘은 형태에서 차이가 있다. 그래파이트는 탄소 여섯 개로 이뤄진 고리가 연결되어 층을 이룬 모양이고 그래핀은 탄소 원자들이 모여 2차원 평면을 이루고 있다. 그래핀 특성을 이용해 백금이 탄소 지지체 위에 ... ...

- UAE 첫 우주인 곧 탄생…러시아 소유즈호 타고 우주정거장으로동아사이언스 l2019.02.26
- 머문다. 8일 후 다른 한 명이 바통을 이어받아 UAE의 두번째 우주인이 될 예정이다. 현재 둘은 러시아 모스크바 근처 스타시티 우주센터에서 우주 생존 기술을 배우고 있다. 알 만수리씨는 “나는 파일럿이기 때문에 내 몸무게의 9배인 G-9까지 중력을 버틸 수 있고 현재는 거의 중력이 없는 상태에서 ... ...

- 3D 프린팅 기술로 휘어진 코뼈 고친다동아사이언스 l2019.02.25
- 새로운 기술을 학계에 보고했다. 사람의 코 중앙에 수직으로 위치해 콧구멍을 둘로 나누는 칸막이인 비중격은 대부분 약간씩 한쪽으로 휘어져 있다. 하지만 휘어짐이 심각하면 코막힘, 수면장애 등 질환이 동반된다(비중격 만곡증). 건강보험심사평가원에 따르면 2016년 기준, 5만 명이 넘는 ... ...
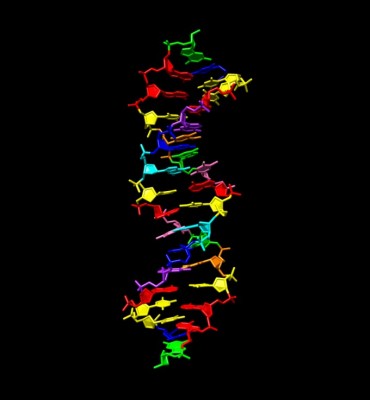
- 유전 정보 저장 능력 커진 ‘인공 DNA’ 탄생동아사이언스 l2019.02.25
- 이 염기들은 기존 염기들처럼 2개씩 짝을 이뤄 상보적(마치 열쇠와 열쇠구멍처럼 둘끼리만 결합)으로 결합하며 단백질을 합성하기 위해 RNA를 만드는 정보 전환 단계도 안정적으로 거쳤다. 다만 새 DNA를 갖고 독자적인 생명체로 자랄 가능성은 없다고 밝혔다. 벤너 위원은 “인공 염기와 단백질을 ... ...

- [내 마음은 왜 이럴까?]진실을 대하는 인간의 속성 '라쇼몽 효과'2019.02.24
- 8시에 시작되는 풋볼 경기였죠. 얼른 경기를 보고 싶으니 성급한 결정을 내린 것입니다. 둘째 자신이 믿고 싶은 진실과 자신이 서로 관련되어 있는 것은 아닌지 의심하는 것입니다. 만약 판단의 대상이 되는 사람과 동일한 집단에 있거나, 같은 처지에 있거나, 과거에 비슷한 경험을 한 적이 있다면, ... ...

- 일상용품을 예술 작품으로~ 마르셀 뒤샹의 ‘샘’수학동아 l2019.02.23
- 때 오히려 수학과 철학 토론에 열광했습니다. 당대를 지배하고 있던 예술에서 거리를 둘 수 있기 때문이지요. 특히 ‘리만 기하학’에 ‘진심으로’ 빠져 있었습니다. 기존의 개념을 완전히 바꾸는 것을 좋아했던 뒤샹이었기에, 그에게 타원 공간에서 펼쳐지는 리만 기하학은 너무나도 아름다운 ... ...
이전878889909192939495 다음

















