뉴스
"그림"(으)로 총 2,148건 검색되었습니다.
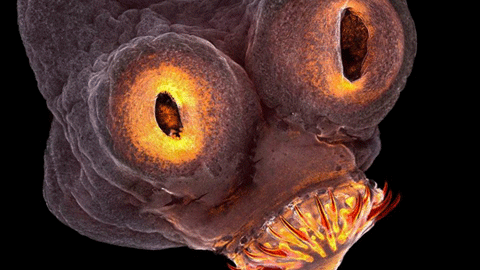
- 기생충 얼굴은 어떻게 생겼을까? 기생충 얼굴 확대 사진팝뉴스 l2017.09.14
- 위 사진이 수상작 중에서 큰 주목을 받는 것이다. 우주 괴물일까? 누군가 그린 그림일까? 아니도 우리의 몸이 아주 익숙한 생명체일 것이다. 바로 촌충이다. 이 기생충의 얼굴을 확대하니 무섭고 무섭다. ※ 편집자주 세상에는 매일 신기하고 흥미로운 일이 많이 일어납니다. 보는 이의 눈살을 ... ...

- [예술] 다람쥐가 나비 날개를 달았다팝뉴스 l2017.09.14
- 가장 큰 특징은 거북을 지구 혹은 ‘대자연 어머니’로 여긴다는 점이다. 리사 에릭슨의 그림에서는 세상의 만물, 세상의 살아 있는 많은 것들이 거북 등에 올라가 있다. 거북이 나비를 업고 다니는 이미지가 많은데, 주목을 끄는 한 작품에서 예술가는 다람쥐에게 나비 날개를 달아주었다. 어떤 ... ...

- 무게중심을 잡아라!어린이과학동아 l2017.09.13
- 꽂고 ②의 과정을 반복한다. ➍ 연필이나 손가락으로 두 개의 선이 만나는 점에 대고 그림을 받친다. 원리 무게중심을 영어로 하면 ‘center of gravity’, 즉 중력이 모이는 지점이다. 그래서 물체의 여러 지점에서 중력이 어느 방향으로 쏠리고 있는지 알면 무게중심 을 찾을 수 있다. 이 실험에서는 ... ...

- 문신잉크, 피부에 남지 않고 몸 속을 돌아다닌다동아사이언스 l2017.09.12
- 끌고 있습니다. 기자도 한 번쯤은 시도할까 생각해 본적이 있고요. 영구적으로 피부에 그림이 남는 것에 매력을 느끼기도 하지만, 바로 이 점 때문에 부작용이 생기기도 합니다. 피부에 바늘로 구멍을 뚫어 잉크를 주입하기 때문에 문신 시술을 받고 나면 상처가 나고 염증이 생길 수도 있습니다. ... ...

- [강석기의 과학카페] 게놈편집으로 흰 나팔꽃 만들었다!2017.09.12
- 색소를 못 만들어 흰 꽃이 필 것이라고 예상했다. 사실 흰 나팔꽃은 1631년 그려진 그림 속에서 처음 등장했다. 즉 일본에 나팔꽃이 소개된지 대략 850년 뒤에 변종이 등장한 것이다. 이후 게놈 분석을 통해 DFR-B 유전자의 돌연변이로 효소가 작동을 못하면서 흰 나팔꽃이 나왔다는 사실이 밝혀졌다. ... ...

- 초현실적이면서 극사실적인 작품들팝뉴스 l2017.09.06
- 물론 모두 연필로 그린 흑백의 작품들이다. 화가가 이 초현실적이고 극사실주의적인 그림을 그리는 이유, 그것도 연필을 이용하여 흑백으로만 그리는 이유는 무엇일까? 직접 들어보자. “저는 예술에서 한계를 깨는 걸 좋아합니다. 그리고 제게는 이것이 한계를 깨는 한 방법이지요. 이것이 내 ... ...

- 수학으로 탄생한 ‘인생샷’ 제조 앱수학동아 l2017.09.06
- 할지 줄여야 할지 알려주고, 원 바깥쪽 화살표(②)가 얼굴의 위치를, 화면 왼쪽 상단 태양 그림과 함께 있는 화살표(③)가 광원의 위치를 어디로 옮겨야 할지 가르쳐 준다. - ⓒDaniel Vogel 제공 잘 나온 셀카를 뜻하는 ‘인생샷’을 건지려면 사진을 수십장 찍는 노력이 필요해요. 이를 도와줄 스마트폰 ... ...

- [강석기의 과학카페] 객성과 신성과 초신성2017.09.05
- 읽으면 가슴이 뭉클하다. 격변변광성이 신성 폭발을 일으키는 메커니즘을 도식화한 그림이다. 근접쌍성계에서 적색거성 같은 동반성(왼쪽)에서 백색왜성(가운데 네모 안)으로 물질이 유입될 경우 별 표면 온도가 올라가 수소융합반응이 일어나면서 껍질이 폭발한다. 오른쪽은 백색왜성 부분을 ... ...

- 고대 로마의 영토를 지하철 노선도로 표현팝뉴스 l2017.08.31
- 도로망을 요즘 사람들 눈에 확 들어오게 설명하는 방법이 무엇일까 하고 고민한 끝에 그림과 같은 작품을 만들어냈다. 즉 전철 노선으로 표현한 로마의 도로망이다. 그녀가 만든 로마전철 노선도는 지중해세계를 하나의 도시로 축소한 느낌을 준다. 중앙에 ‘내해 Mare Internum’란 이름의 거대한 ... ...
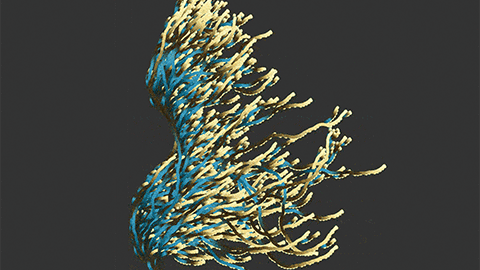
- 수학의 변신은 무죄! 예술이 된 난제수학동아 l2017.08.30
- 알렉스 벨로스는 콜라츠 추측이 얼마나 풀기 어려운지 보여주기 위해 콜라츠 추측을 그림으로 나타냈어요. 콜라츠 추측은 1937년 독일 수학자 로타르 콜라츠가 제시한 문제로, 어떤 자연수든지 짝수면 2로 나누고 홀수면 3을 곱한 뒤 1을 더하다 보면 결국 1이 된다는 추측이에요. 예를 들어 3은 7번(3→ ... ...
이전132133134135136137138139140 다음

















