스페셜
"정신이상"(으)로 총 433건 검색되었습니다.

- 공감 능력이 없는 반사회성 인격장애, 어떻게 봐야 할까?KISTI l2015.03.31
- 여러 반사회적인 사건으로 사회가 소란스럽다. 인질 삼은 의붓딸 가족을 성폭행하고 살해한 40대 남성, 구토한 어린이를 달래주기는커녕 다시 그것을 집어 먹게 한 어린이집 교사, 자신의 심기를 건드렸다는 이유로 출발한 비행기를 돌려 세운 대기업 총수의 장녀. 이처럼 다른 사람의 권리를 무 ... ...

- 양자역학 도약 이끈 슈뢰딩거방정식은 ‘간통’ 덕분?2015.03.02
- 그와의 만남에 그녀는 수줍어 고개 숙였고… 그의 소심함에 그녀는 떠나가 버렸다 - ‘화양연화’ 왕가위 감독의 2000년 작품 ‘화양연화’는 간통을 소재로 하고 있다. 영화의 배경은 1962년 홍콩. 거실과 주방을 공유하는 공동주택으로 같은 날 이사를 온 차우모완(양조위)과 첸 부인(장만옥)은 동 ... ...

- 귀신의 과학KISTI l2015.02.24
- KISTI 과학향기 제공 새벽 1시. 야근을 마치고 불이 꺼진 컴컴한 건물 복도를 홀로 걷고 있는데, 갑자기 등 뒤에 누군가가 있다는 느낌이 든다. 흠칫 놀라며 뒤를 돌아보았으나 아무 것도 보이지 않는다. ‘유령이었나?’라고 혼자 중얼거리며 다시 걷기 시작하지만, 왠지 모골이 송연해진다. 누구나 ... ...

- 암은 여전히 은유로서의 질병인가2015.02.16
- 질병은 그저 질병이며, 치료해야 할 그 무엇일 뿐이다. - 수전 손택 ‘뉴욕 지성계의 여왕’으로 불리며 미국 최고의 문필가로 이름을 날린 수전 손택(Susan Sontag)은 글을 쓰는 직업을 꿈꾸는 많은 여성들의 롤모델일 것이다. 손택은 에세이, 소설, 희곡 등 다양한 분야에서 활약했는데 특히 에세 ... ...

- 과학은 길고 인생은 짧다 [2회]2014.12.29
- 2014년은 국내외에서 유난히 사고가 많은 해였다. 보통 연말이면 한 해가 가는 게 아쉬울 법도 하지만 올해는 더 이상 사고 없이 빨리 지나갔으면 하는 바람이다. 2014년 타계한 과학자 가운데도 사고나 스캔들로 인한 죽음이 있었다. 에이즈 분야의 석학인 네덜란드의 욥 랑게 교수는 지난 7월 17일 ... ...

- [만화] 우황청심원은 시험의 긴장을 풀어줄 수 있나?KISTI l2014.12.22
- KISTI 과학향기 제공 태연이 일 년에 딱 한 번 알람 없이도 침대에서 벌떡 일어나는 아침이 있으니, 바로 대학수학능력시험(이하 수능)을 치르는 날이다. 집 앞에 바로 고등학교가 있어, 수능 날이면 선배들을 응원하는 후배들의 어마어마하고 무시무시한 응원 소리와 북소리에 꿀 같은 아침잠을 포기 ... ...
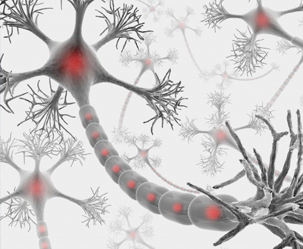
- 뇌는 정말 신체적 고통과 정신적 고통을 구별하지 못할까?2014.12.01
- 물리학이나 화학의 최신 연구결과들이 대중의 관심을 끄는 경우는 드문 것 같다. 내용을 이해하기가 어렵기도 하지만 그 결과가 일상생활과 무관한 경우가 대부분이기 때문이다. ‘그들만의 리그’인 셈이다. 반면 생명과학 분야는 좀 다른데 우리자신이 생물인데다 연구의 상당부분이 의학, 즉 건 ... ...
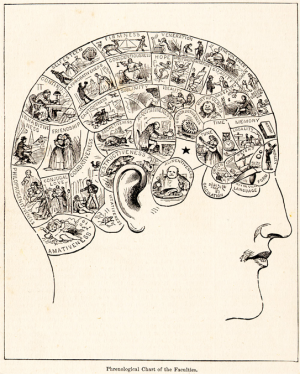
- 장님 코끼리 만지기 : 뇌와 의식을 이해하려는 노력들IBS l2014.10.08
- "우리가 두뇌를 이해할만큼 두뇌가 단순했다면, 우리는 너무 단순해서 두뇌를 이해할 수 없었을 것이다." 남아프리카 공화국의 생물학자인 라이얼 왓슨이 남긴 말이다. 왓슨은 뉴에이지에 경도된 면이 있어 호불호가 갈리는 사람이기는 하지만, 그의 말은 뇌가 얼마나 복잡한 기관인지 보여준다. ... ...

- 1976년 에볼라 역병은 어떻게 시작되었나2014.08.04
- 어머니는 늘 저에게 ‘웅변은 은이고 침묵은 금’이라고 가르치셨죠. 하지만 전 차마 말로 할 수 없는 광경을 너무나 많이 보았습니다. - 페터 피오트, 에볼라 바이러스를 처음 관찰한 바이러스학자. 필자가 단골로 가는 카페에서는 주인장이 커피 마니아라서인지 매주 스페셜 커피를 내놓는 ... ...

- [MATH] 반(半) - 자장면과 종이접기KISTI l2014.07.21
- 우리는 종종 어떤 것을 반으로 나누는 것을 대수롭지 않게 여긴다. 하지만 자연수 중에서 1을 제외하고 가장 작은 수 2와 그것의 역수인 ‘반’, 즉 1/2의 위력은 우리가 생각하고 있는 것 이상으로 대단하다. 종이접기를 이용하여 반으로 나누는 것에 관하여 알아보자. 외국에서는 이 종이 반접기가 ... ...
이전353637383940414243 다음

















