뉴스
"1"(으)로 총 33,812건 검색되었습니다.

- 최근 10년간 20~30대 여성 음주 늘었다...여성 고위험음주도 증가동아사이언스 l2023.10.30
- 남자는 61.7%에서 56.0%로 유의하게 감소했다. 여자는 31%에서 31.1%로 큰 변화가 없었다. 1회 음주량이 남자는 5잔, 여자는 3잔 이상을 주 4회 이상 마신 분율인 '지속적 위험음주율'은 남자는 10%, 여자는 3% 내외로 연도별 증감을 반복했다. 남자는 50~60대, 여자는 30대에서 가장 높았다. 담배와 ... ...

- '번개맨'처럼 체온으로 전기 생산…전지 효율 높인다 동아사이언스 l2023.10.30
- 대비 2배 이상 높은 에너지 전환 효율을 보였다. 또 이를 통해 전극 제작 단가를 3000분의 1로 줄이는 데 성공했다. 김 교수는 "상대적으로 많이 연구되지 않았던 열-전기화학 전지의 촉매 연구를 통해 시스템의 효율성과 경제성을 모두 향상시켰다"며 "폐열로 에너지를 생산하는 에너지 하베스팅 ... ...
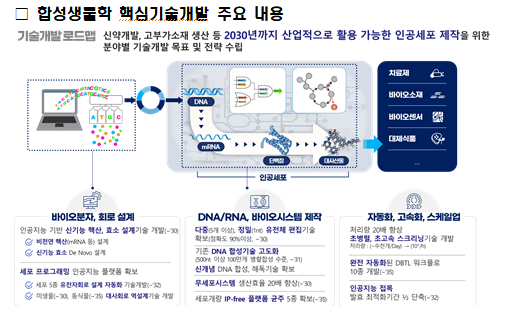
- 합성생물학, 2030년까지 선도국 90% 수준으로 키운다동아사이언스 l2023.10.30
- 대해 함께 논의했다. 이날 발표된 ‘합성생물학 핵심기술개발 및 확산전략’은 11월 개최 예정인 생명공학종합정책심의회에서 구체적인 내용이 확정된다. 과힉기술정보통신부 ... ...
- [바꿔쓰자!과학용어] ④트라이글리세라이드→중성지방…의료 부문 건강검진용어동아사이언스 l2023.10.30
- 관계자의 설명이다. 신사구체여과율은 신장 기능을 평가할 수 있는 수치로, 신장이 1분간 깨끗하게 걸러낸 혈액의 여과율을 의미한다. 신사구체는 신장의 사구체를 의미하는 단어로, 사구체는 혈액을 여과하는 조직체다. 이 한자어를 대체할 적절한 한글 표기는 아직 없다. 감마지티피는 간 ... ...

- "기후데이터 생산 1분만에 제공...전세계 예측 데이터도 수집"동아사이언스 l2023.10.30
- 연결되도록 데이터 실시간 연계 체계인 에이피아이(API) 서비스를 확대한다. 2018년 21종으로 시작한 에이피아이(API) 서비스는 2023년 156종으로 확대됐다. 그동안 기상청은 API로 데이터만 제공했다. 앞으로는 데이터를 가시화한 그래픽 에이피아이(API)도 함께 제공하게 된다. 대용량 데이터 전처리부터 ... ...

- "초기 금성에서 '대륙 이동' 있었다… 생물체 존재했을 수도"동아사이언스 l2023.10.29
- 또 금성의 판 이동은 초기 지구와 동시간대에 발생했을 수 있다고 설명했다. 논문 1저자인 매트 웰러 박사후연구원은 "오늘날 지구 생명체의 생존을 가능케 한 판 활동과 같은 체계가 금성에도 동시에 존재했다"라며 초기 금성에 지구와 비슷한 형태의 미생물이 존재했을 가능성을 높였다고 ... ...

- 소 럼피스킨병, 열흘만에 전국 60건…확산세 이어질듯동아사이언스 l2023.10.29
- 10% 이하이며 인수공통감염병이 아니어서 사람에게 옮기지 않는다. 20일을 시작으로 21일 3건→22일 6건→23일 7건→24일 12건→25일 9건→27일 5건→28일 8건 등 날마다 발병 사례가 보고됐으며 지역별로는 충남, 경기, 인천, 충북, 강원, 전북 등 6개 시도 농장에서 확진 사례가 나왔다. ... ...

- 구름 만드는 '비밀의 방', 인공강우 가능성 열었다동아사이언스 l2023.10.29
- 있는 첫 걸음을 내딛었다는 점에서 의미가 있다"고 말했다. 이번 연구 결과는 오는 11월 1일부터 3일까지 부산 벡스코에서 열리는 2023년 한국기상학회 가을학술대회에서 발표될 예정이다. 구름물리실험챔버 개요. 한국기상학회 제공 ... ...

- [표지로 읽는 과학] 생명유지의 핵심, 뇌의 작은 방 '시상하부'동아사이언스 l2023.10.29
- 불과한 시상하부는 복잡한 구조로 이뤄져 있다. 좌우에 한 쌍으로 존재하는 시상하부는 11개의 핵을 갖고 있다. 대뇌와 뇌줄기 사이를 연결하는 부분은 많은 신경섬유로 구성됐다. 시상하부의 가장 중요한 역할은 뇌하수체를 통해 신경계를 내분비계와 연결하는 것이다. 이를 통해 우리 몸에서 ... ...

- 조선의 '코페르니쿠스'로 불린 홍대용과학동아 l2023.10.28
- 1율:2율 = 3율:4율 이라는 식에서 1, 2, 3율은 아는 수, 4율은 미지수일 때, 4율 = (2율×3율)/1율 이라는 식으로 미지수를 구하는 풀이법이다)이라 불리는 비례식을 풀이법으로 제시했다. 정말 홍대용이 서양 수학을 깊이 이해하지 못해서 사율법을 풀이로 대신 내놨던 것일까. 사실 홍대용이 다룬 ... ...
이전455456457458459460461462463 다음

















