뉴스
"평면"(으)로 총 363건 검색되었습니다.
- 3D 프린팅 넘어 ‘4D 프린팅’ 온다 2015.02.13
- e메일 인터뷰에서 “자체 개발한 프로그램에 원하는 모양을 입력하면 컴퓨터가 스스로 평면 설계도를 만들어 내는데, 이걸 출력해서 오븐에 넣기만 하면 물건이 나온다”면서 “무생물인 물질에 생명을 불어넣는 4D 프린팅 연구에 관심이 높아지면서 미국과학재단(NSF)도 3000만 달러(약 330억 원) ... ...

- 뜨개질 도와주는 수학2015.01.21
- 것은 어떨까. ‘힐베르트 곡선’으로 평면을 채우면 여러 가지 패턴을 만들 수 있다. 평면을 격자로 나타내고 모든 칸의 중심을 한 번씩 지나도록 끊어짐 없이 선을 그리면, 패턴을 만들 수 있다. 격자 중심에서 상하좌우의 방향으로 이동하며 힐베르트 곡선을 그리고 이어 붙였더니 하나의 ... ...

- 피타고라스정리를 알면 최선의 치료방법이 보인다2015.01.19
- 길이의 제곱은 나머지 두 변의 길이의 제곱의 합과 같다’는 피타고라스의 정리는 좌표평면에서 두 점 사이의 거리를 구할 때도 쓰인다. - 위키피디아 제공 책 6장 ‘입 밖에 낼 수 없는 것’은 무리수에 대한 이야기다. 피타고라스가 이집트 사람들이 발견한 변의 비가 3:4:5인 ‘황금비’ ... ...

- 뒤틀리는 비누막의 비밀2015.01.14
- 이때 작용하는 표면장력과 저항력을 측정했다. 그 결과 고리의 길이가 길어지면 평면이었던 비누막이 아령 모양으로 바뀌었다. 고리의 길이가 늘어남에 따라 저항력이 감소하기 때문이다. 한편, 고리를 비틀었을 때는 반대로 저항력이 증가하면서 비누막이 아예 뒤틀렸다. 비누막은 생체막의 ... ...

- 초소형 3층 건물 만드는 비법2015.01.11
- 마이크로미터 크기의 3차원 구조물들을 구경하는 재미가 쏠쏠하다. 연구진은 2차원 평면 위에 재료를 기하학적으로 깔아 놓은 뒤에 인위적인 힘을 가해서 원하는 모양의 3차원 구조를 만드는 방법을 개발했다. 예를 들어 십자가 모양으로 배치한 물질을 동서남북 방향에서 힘을 가해 불룩 ... ...

- 이번엔 무슨 그래핀? ‘포스트 그래핀’!2015.01.09
- 차원 금속 칼코겐. 금속(티타늄, 몰리브덴 등)과 칼코겐 원소(황, 셀레늄 등)가 2차원 평면구조를 만들었다. 강도가 높고 유연하면서도 반도체적인 특성이 뛰어나다. - 연세대 화학과 제공 국내 연구팀이 ‘포스트 그래핀’이라 불리는 2차원 단일층 나노물질을 쉽고 간단하게 생산할 수 있는 기술을 ... ...

- 이제는 입체가 대세, 3차원 그래핀 온다2014.11.10
- 방법을 이용해 원하는 모양을 만들기가 어렵고, 일단 입체구조로 만들어도 다시 2차원 평면구조로 돌아가려는 습성이 강해 불안정한 문제가 있었다. 연구팀은 먼저 고출력 반도체 소자에 흔히 쓰이는 실리콘 카바이드로 3차원 그래핀의 주형이 되는 탄소구조체를 만들었다. 그리고 탄소구조체를 ... ...
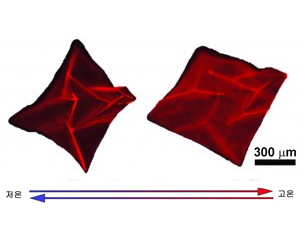
- 종이처럼 접히는 마이크로 로봇 나왔다2014.11.06
- 25도로 떨어지면 주위 수분을 흡수해 팽창하며 로봇으로 변한다. 온도를 다시 올리면 평면으로 돌아간다. 게다가 하이드로젤 스마트 시트의 구성 성분에 변화를 주면 변하는 온도를 조절할 수도 있다. 그동안 종이접기 로봇은 주로 형상기억합금 소재를 이용해 만들었다. 하지만 형상기억합금은 ... ...
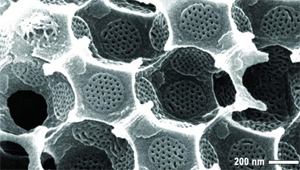
- 맨홀뚜껑 닮은 나노구조로 뭐 만들까2014.10.28
- nm는 10억 분의 1m) 크기의 구멍을 맨홀뚜껑 모양으로 낸 고분자물질을 채워 넣었다. 기존 평면(2차원) 구조였던 분리막을 3차원 구조로 만들면서 두께는 두꺼워졌지만 표면적이 넓어져 처리 속도가 빨라지고 내구성도 높아졌다. 유 교수는 “이번에 개발한 구조를 이용하면 더 튼튼하면서도 ... ...

- 한가위 보름달은 수학으로 뜬다!수학동아 2014.09.06
- 증명했다. 그 이후에는 불규칙한 다각형도 구적 가능함을 밝혀냈다. 직선으로 된 평면도형이 모두 구적가능하다는 것이 증명되자, 수학자들은 곡선으로 된 도형이 구적 가능한지 생각하기 시작했다. 그리고 한 수학자가 곡선으로 된 구적 가능한 것을 찾았는데, 그가 바로 히포크라테스다. 당시 ... ...







